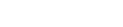1到365依次相加等于多少
根据题意列式得:
1+2+3+……+365
=(1+365)×182+183
=66795
解题思路是,我们把靠前个数字和最后一个数字相加等于366,第二个数字和倒数第二个数字相加也等于366,第三个数字和倒数第三个数字相加还是等于366,直到第182个数字和倒数第182个数字即184相加仍然等于366,然后再加上在中间的数字183,就可以得到答案是66795。
答:1加到365求和这是等差数列求和问题。可以这样算:(1+365)×365÷2=366×365÷2=56795。这是高中数学教学内容。现在你明白了吗?
最后结果等于66795。
1+2+3+……+365
=(1+365)×365÷2
=366×365÷2
=133590÷2
=66795
从1加到365就是一个等差数列的相加,总和利用等差数列求和公式得到:
=(1+365)*365/2。
=66795。
解释分析:
该题需要使用求和公式:
若一个等差数列的首项为a1,末项为an那么该等差数列和表达式为:
即(首项+末项)×项数÷2。
其他推论:
1、和=(首项+末项)×项数÷2。
2、项数=(末项-首项)÷公差+1。
3、首项=2x和÷项数-末项或末项-公差×(项数-1)。
4、末项=2x和÷项数-首项。
5、末项=首项+(项数-1)×公差。
6、2(前2n项和-前n项和)=前n项和+前3n项和-前2n项和。
等于50370。365X(1十365)/2=365X183。而365X138=50370。这是利用非0自然数相加公式计算而得。1十2十3十……十n=n(n十1)/2计算而成。